Fachbegriffe der Musiktheorie mit Hörbeispielen
| Home | Index | Literatur | Dokumente | Kritik | Kontakt |
Modulation ist der harmonische Übergang von einer Tonart zur andern. Ein einfaches Beispiel ist die folgende Modulation von a-Moll nach C-Dur:
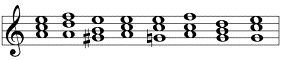
Das Ohr haust sich hier zunächst im Tonbestand von a-Moll ein, wird dann aber durch den Ton g aus dieser Tonart herausgerissen. Sofern nicht noch weitere Töne außerhalb der Tonart a-Moll auftreten, unterstellt die Wahrnehmung eine Tonart, welche erstens die mit dem g auftretenden Töne enthält und zweitens maximale Übereinstimmung mit dem Tonbestand der vorausgehenden Tonart aufweist. Diese Tonart ist im vorliegenden Fall C-Dur. Die genauere Untersuchung der Modulation ist zusammengefasst in den Gesetzen der Modulation, auf deren Grundlage sich Musikstücke harmonisch analysieren lassen.
In der Modulation realisiert sich ein harmonisches Verhältnis zwischen den Tonarten. Dieses Verhältnis baut auf der Harmonie der Töne (Konsonanz) und der Harmonie der Konsonanzen (Tonalität) auf und ist somit Harmonie in einer dritten Dimension: Die Tonbestände der Tonarten harmonieren aufgrund ihrer gemeinsamen Töne. Der gängige Ausdruck für diese Harmonie ist Verwandtschaft der Tonarten.
Mehr zu diesem Thema in dem Artikel Modulation laut Wikipedia.
Eine zusammenhängende Analyse der Modulation findet sich in Musikalisches Grundwissen.
 |
 |
 |
 |
Die Verwandtschaft der Tonarten beruht auf der Übereinstimmung ihrer Tonbestände. Der Tonbestand einer Tonart ergibt ich aus seinen tonalen Komponenten. In der Modulation findet ein Wechsel statt zwischen diesen Tonbeständen und der darin verkörperten Tonalität. Damit wird auch ein anderer Dreiklang zur Tonika.
Die Übereinstimmung zwischen zwei Tonarten ist im Folgenden am Verhältnis zwischen C-Dur und a-Moll demonstriert:
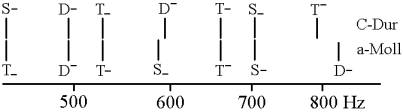
Die harmonisch jeweils unterschiedlich bestimmten Töne (kenntlich an den Formeln) stimmen beim harmonischen Vergleich der Tonbestände überein, wenn sie auf nahezu oder absolut identischer Frequenz liegen. Im vorliegenden Fall haben die Tonarten sechs gemeinsame Töne, wobei die Töne mit 586,67 Hz und mit 594 Hz (beide heißen d) als identisch gelten. Ihre geringfügige Differenz, die für die Unterscheidung von Tönen keine Rolle spielt, heißt in der Musik Komma. Die Töne mit 586,67 Hz und 594 Hz differieren um das so genannte syntonische Komma (81:80).
Betrachtet man die beiden obigen Tonarten, so hat jede sieben Töne, aber sie bilden ein System von acht Tönen, in dem beständig zwischen a-Moll und C-Dur moduliert werden kann. Bezieht man weitere Tonarten ein, die mit diesen Tonarten und untereinander mehr oder weniger übereinstimmen (= verwandt sind), so ergibt sich ein geschlossenes System von zwölf Tönen, aus dem keine Modulation herausführen kann. Die zwölf Töne haben also ihren Grund im Prinzip der Modulation, somit in der Harmonik der Tonarten-Verwandtschaft. Auf diesem Prinzip beruht auch das System der 24 Tonarten:
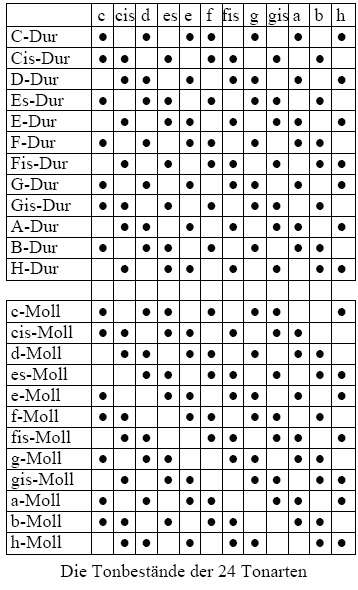
Diese Darstellung abstrahiert – wie die Wahrnehmung selbst – von den unterschiedlichen Stimmungen, die ein Ton vor und nach einer Modulation haben kann. In der Musik ist diese Abstraktion sogar in ein einheitliches und starres System gegossen: die temperierte Stimmung.
Aus der obigen Tabelle lässt sich der Verwandtschaftsgrad der Tonarten ersehen: das Maß der Übereinstimmung der tonartlichen Tonbestände. Diese Abstufung der Verwandtschaft ist wichtig bei der Modulation, weil hier das Prinzip der maximalen Übereinstimmung gilt. Ein Klang mit neuen Tönen kann nämlich oft in mehreren Tonarten vorkommen. Die Modulation ist aber immer ein Übergang in die harmonisch näher liegende Tonart. Kommen mehrere Tonarten mit gleicher Verwandtschaft zur vorausgehenden Tonart in Frage, bleiben die Klänge so lange harmonisch unbestimmt (tonal indifferent), bis sich durch weitere Töne eine Tonart herauskristallisiert, die eindeutig identifizierbar ist. Das Nähere ist ausgeführt in den Gesetzen der Modalition.
|
|
|
|
|
Aus dem Begriff der Modulation lassen sich die folgenden Gesetze ableiten:
1. Eine Tonart konstituiert sich durch das Auftreten von Tönen, die nur dem Tonbestand einer Tonart exklusiv angehören können.
2. Vor der Konstitution einer Tonart (im Zustand der tonalen Indifferenz) kann keine Modulation (= Übergang in eine andere Tonart) stattfinden.
3. Eine Tonart wird verlassen durch das Auftreten von Tönen, die nicht zum Tonbestand dieser Tonart gehören.
4. Ein Klang, mit dem eine Tonart verlassen wird, setzt eine neue Tonart in Kraft, wenn der Tonbestand dieser Tonart erstens diesen Klang enthält und zweitens mehr Töne mit dem Tonbestand der verlassenen Tonart gemeinsam hat als alle andern Tonarten, in denen dieser Klang vorkommen kann (Gesetz der maximalen tonalen Übereinstimmung bzw. der Trägheit des harmonischen Hörens).
5. Wird eine Tonart durch einen Klang verlassen, der in mehreren Tonarten vorkommen kann, von denen sich keine durch größere Verwandtschaft mit der verlassenen Tonart hervortun kann, so entsteht eine tonale Indifferenz.
6. Eine zwischenzeitlich entstandene tonale Indifferenz kann direkt aufgelöst werden durch weitere Klänge, mit deren Hilfe sich die Identität einer neuen Tonart nach dem Gesetz der maximalen tonalen Übereinstimmung herausstellt.
7. Eine zwischenzeitlich entstandene tonale Indifferenz kann indirekt aufgelöst werden durch einen Klang, welcher der Wahrnehmung im Nachhinein eine Folge von zwei Modulationen präsentiert, die in ihrer Gesamtheit eine maximale tonale Übereinstimmung aufweisen.
8. Eine tonale Indifferenz kann durch weitere indifferente Klänge, die einem wechselnden Spektrum von Tonarten angehören könnten, in die Länge gezogen werden, so dass der harmonische Zusammenhang zu der verlassenen Tonart verloren geht (Beispiel: halbtonweise versetzte [=chromatische] Folge von verminderten Septakkorden).
9. Wird eine Tonart durch einen Klang verlassen, der in keiner Tonart vorkommen kann, so geht durch diesen atonalen Klang der Zusammenhang mit der verlassenen Tonart verloren.
10. Der verlorene Zusammenhang mit einer verlassenen Tonart schließt zunächst jegliche Modulation aus und erfordert die erneute Konstitution einer Tonart (siehe Punkt 1).
Die Berücksichtigung dieser Gesetze ist Voraussetzung für die korrekte harmonische Analyse eines Musikstücks. Die gewöhnliche Vorstellung von der Modulation operiert mit dem verkehrten Begriff der Umdeutung.
Die Ableitung dieser Gesetze aus dem Prinzip der Modulation sowie die genauere Darstellung anhand von Noten-Beispielen findet sich im 3. Kapitel des Buchs "Die tonale Musik".
|
|
|
|
|
Begriff, der in der Musikwissenschaft eingeführt wurde, um den Vorgang der Modulation zu erklären. Der Haken dabei ist, dass jede Definition der Modulation, welche diesen Begriff zu Hilfe nimmt, den Vorgang der Modulation bereits als Voraussetzung der Umdeutung unterstellt. Hugo Riemann zum Beispiel definiert die Modulation als
"Gewinnung einer neuen Tonika vermittelst Umdeutung von Harmonien aus Funktionen der alten Tonart zu solchen der neuen." (Hugo Riemann, Handbuch der Harmonielehre, Leipzig 1918, S. 216)
Wenn HarmonienWenn Harmonien "zu solchen der neuen" Tonart umgedeutet werden sollen, so muss man sich fragen, wie es denn zu der neuen Tonart kommt, welche den Harmonien eine neue "Bedeutung" gibt. Die Antwort: "vermittelst Umdeutung" – und die Sache dreht sich im Kreise. Die Umdeutung soll die Modulation erklären und die Modulation die Umdeutung.
Mehr zu diesem Thema in dem Artikel Modulation laut Wikipedia.
|
|
|
|
|
Viele Musiktheoretiker begreifen die Modulation nicht einfach als Wechsel der Tonart, sondern als besondere Form, in der dieser Wechsel vonstatten geht: Er soll angeblich "allmählich" stattfinden. Das entgegengesetzte Konstrukt ist die Rückung, worin der Wechsel "plötzlich" erfolgen soll. So hieß es 2013 noch bei Wikipedia:
"Unter einer Rückung versteht man in der Harmonielehre den plötzlichen, abrupten Wechsel des tonalen Zentrums ... im Gegensatz zur Modulation..."
2016 findet man dort unter der Bitte um Überarbeitung einen anderen Versuch der Definition:
"Unter einer Rückung versteht man in der Harmonielehre die unvermittelte Verschiebung des tonalen Zentrums (Tonika), anders als bei der vermittelnden Modulation, bei welcher der Wechsel der Tonart durch Fortschreitungen vollzogen wird."
Wie auch immer der Streit der Autoren weitergehen wird: Er dreht sich um eine Sache, die es nicht gibt. Die Vorstellung einer Rückung unterstellt die Vorstellung einer Modulation, die nicht durch Töne außerhalb der bisherigen Tonart bewirkt wird, sondern durch mystische Vorgänge, die eben schwer zu definieren sind.
|
|
|
|
|
Unter dem Titel Zwischendominante wird die Dominante einer neuen Tonart als ein Akkord angesehen, der noch immer zur alten Tonart gehört. Jede Definition der Zwischendominante bestreitet ausdrücklich, dass die Tonart gewechselt wurde, obwohl zugleich zur Kenntnis genommen wird, dass die Töne dieses Akkords nicht in der alten Tonart vorkommen. Insofern handelt es sich um eines der funktionstheoretischen Konstrukte des alterierten Akkords, bei dem die Tonart prinzipiell getrennt von den Tönen betrachtet wird, aus denen sie besteht.
Mehr zu diesem Thema in dem Artikel Zwischendominante laut Wikipedia.
|
|
|
|
|
Besondere Konstellation bei einer Modulation, worin der letzte Klang der alten Tonart eine markante Dissonanz (will sagen: keine Scheinkonsonanz) ist, und der erste Klang der neuen Tonart eine Tonika. In diesem Fall erscheint die Dissonanz auflösungsbedürftig, solange sie erklingt. Beim Wechsel in die neue Tonart erübrigt sich jedoch ihre Auflösungsbedürftigkeit. Die Tonika der neuen Tonart ist andererseits – weil Tonika – nicht auflösungsbedürftig. Es entsteht dadurch der Anschein, als ob die Tonika der neuen Tonart eine Auflösung der vorangegangenen Dissonanz sei.
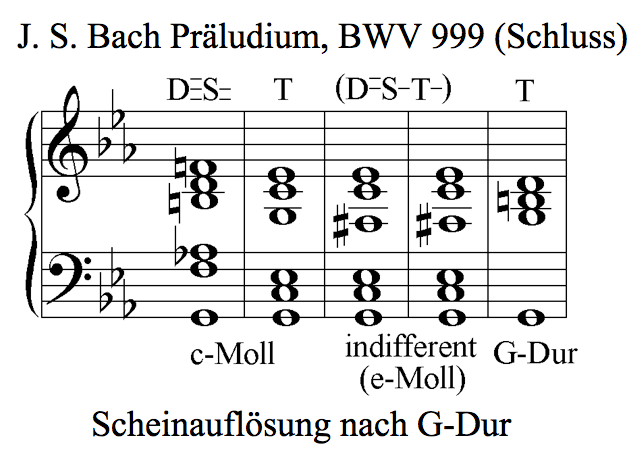
Die Scheinauflösung nährt den Eindruck, dass die scheinbar aufgelöste Dissonanz zur Tonika der neuen Tonart gehöre. Theoretisch profitiert davon die verbreitete Illusion, einer Tonart würden auch „tonleiterfremde“ Töne angehören, also solche Töne, die aufgrund der Harmonik der Tonalität nichts mit dem Tonbestand dieser Tonart zu tun haben. Vor allem speist sich dieser Irrtum aber aus der Verwechslung der Modulation mit der Form, den dieser harmonische Vorgang auf der Ebene der Melodik annimmt: der Alteration. Im Konstrukt des alterierten Akkords wurde diesem Irrtum ein Denkmal gesetzt.
|
|
|
|
|
Tonale Analyse eines Musikstücks
Die folgende (von einem Computerprogramm erstellte) Analyse gibt unten die Tonarten an, die aufgrund der Gesetze der Modulation aus der Harmonienfolge zu erschließen sind. Oben wird für die tonartlich bestimmten Klänge deren tonale Zusammensetzung durch eine harmonische Formel angegeben.
Johann Sebastian Bach, Das wohltemperierte Klavier I, BWV 846 (vereinfachte Notierung)
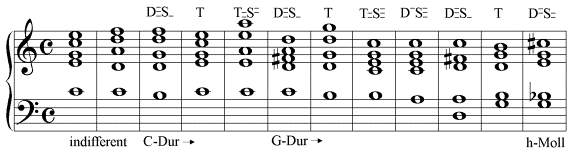
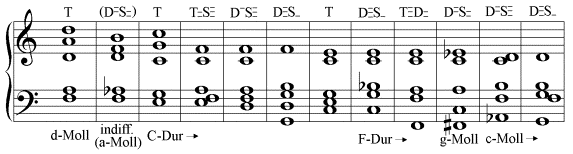
- Takt 1-2: Indifferenz nach dem 1. Gesetz, denn es käme auch noch F-Dur in Frage.
- Takt 3: Konstitution der Tonart C-Dur nach dem 1. Gesetz.
- Takt 6: Modulation nach dem 4. Gesetz. Dasselbe gilt für fast alle weiteren Modulationen.
- Takt 14: Indifferenz nach dem 5. Gesetz.
- Takt 15: Indirekte Auflösung dieser Indifferenz nach dem 7. Gesetz: Insgesamt betrachtet ist eine Modulation zuerst nach a-Moll und dann nach C-Dur das harmonisch Nächstliegende. Die Notierung des gis von a-Moll als as ist eine schreibtechnisch motivierte enharmonische Verwechslung, von der das Stück noch weitere Beispiele enthält.
- Takt 23-25: Beispiel für eine Scheinauflösung.
|
|
|
|
|
Kaum wahrnehmbare Differenz zwischen zwei Tönen; genau genommen: die Differenz zwischen zwei Stimmungen eines Tons, denn ein harmonisch markantes Tonverhältnis wird erst im Bereich des Halbtons wahrgenommen.
Vom Standpunkt der reinen Stimmung treten bei Modulationen Kommata auf, wo die übereinstimmenden Töne verschiedener Tonarten nicht exakt die gleiche Frequenz haben. Das häufigste Komma ist das syntonische Komma mit dem Schwingungsverhältnis 81:80. Es besteht zum Beispiel zwischen der dissonanten kleinen Terz (32:27) und der konsonanten kleinen Terz (6:5). Denn:
(6:5) x (27:32) = 81:80
Ein Beispiel: Die Töne d-f bilden in a-Moll die kleine Terz der Subdominante (6:5), beim Übergang nach C-Dur jedoch eine Scheinkonsonanz (32:27), die durch Oktavversetzung aus dem Verhältnis des subdominantischen Grundtons zu der drei Quinten weiter liegenden dominantischen Quinte hervorgeht, also der Zweiklang mit der Formel
Das syntonische Komma ist jedoch nicht das einzige Komma in der Musik. Das größte hat das Schwingungsverhältnis 128:125 und kommt zum Beispiel bei einer (rein gestimmten) Modulation von a-Moll nach f-Moll vor:
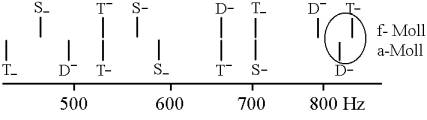
Die beiden Striche im Kreis zeigen die Differenz in der Stimmung des gleichen Tons. Dieses Komma verschwindet in der temperierten Stimmung aufgrund einer gleichmäßigen Verstimmung der Töne:
|
|
|
|
|
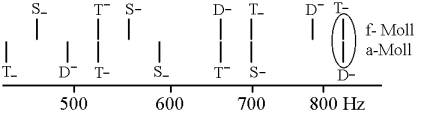
Exakte Höhe eines Tons im Spektrum seiner Schwankungsdifferenzen (Kommata). Vom Standpunkt der reinen Stimmung schwankt die Höhe einzelner Töne infolge der Modulation. Die Abstraktion der Wahrnehmung von diesen Schwankungen in der Tonstimmung ermöglicht eine einheitliche und starre Stimmung der Töne durch die Temperatur.
|
|
|
|
|
Exakte Schwingungsverhältnisse innerhalb des Tonbestands einer Tonart auf Basis der Tonalität und der ihr zugrunde liegenden Frequenzverhältnisse der Konsonanz (3:2, 5:4. 6:5). Da die Stimmung der Töne infolge der Modulation schwanken kann, ist als starre Stimmung die temperierte Stimmung üblich geworden. Die reine Stimmung hat daher fast nur noch eine theoretische Bedeutung, weil sie der temperierten Stimmung zugrunde liegt und zu ihrer Erklärung herangezogen werden muss.
|
|
|
|
|
Bei Instrumenten mit festliegenden Tönen bestand beim Übergang zur tonalen Musik das Problem, dass die reine Stimmung eine Einschränkung auf eine bestimmte Tonart notwendig machte, weil bei der Modulation einzelne Tonstimmungen um ein Komma schwanken können. Man entwarf daher verschiedene "temperierte" Stimmungen, mit denen die Stimmungsschwankungen bei der Modulation ausgeglichen werden sollten. Lange Zeit galt die mitteltönige Temperatur als optimal, da sie der reinen Stimmung (besonders bei den Terzen) sehr nahe kommt. Sie hatte aber den Nachteil, dass sie das Spiel auf den Bereich von wenigen Tonarten einschränkte und außerhalb dieses Bereichs zu Misstönen (sog. Wölfen) führte. Diese Wölfe überschreiten als Verstimmungen die Dimension des Kommas und kommen in den Bereich des wahrnehmbaren Tonverhältnisses (des Halbtons).
Eine wirkliche Lösung des Problems brachte die gleichschwebend temperierte Stimmung, die eine größere Verstimmung der Terzen innerhalb einer Tonart in Kauf nimmt, um jegliche Einschränkung des Modulierens zu überwinden. Die Oktave (2:1) ist bei dieser Stimmung in 12 gleiche Tonverhältnisse unterteilt, die somit das Schwingungsverhältnis 21/12:1 haben. In dieser Stimmung klingen alle Tonarten gleich akzeptabel. Damit werden die in der Modulation als identisch wahrgenommenen Töne auch akustisch einheitlich dargeboten.
| Konsonanz | Reine Stimmung | Gleichschw. Temperatur | Verstimmungsgrad |
| Quinte | 3:2 = 1,5000 | 27/12 = 1,4983 | 1,0011 |
| Große Terz | 5:4 = 1,2500 | 25/12 = 1,2599 | 1,0079 |
Zum Vergleich zwischen rein gestimmten und temperierten Tönen einer Tonart siehe auch: Komma.
|
|
|
|
|
| © 2016 Franz Sauter, Hamburg | Datenschutz |