![]()
Fachbegriffe der Musiktheorie mit Hörbeispielen
| Home | Index | Literatur | Dokumente | Kritik | Kontakt |
Tonalität ist die Harmonie der Tonart. Sie besteht im Harmonieren von Dur- oder Mollklängen, die im Quintverhältnis stehen. Als Bestandteile dieser Harmonie heißen die konsonanten Dreiklänge Tonika, Dominante und Subdominante. Die einfachste Form, in der die Tonalität in Erscheinung tritt, ist die Kadenz. Aber auch die Dissonanz enthält tonale Verhältnisse, insofern die Bestandteile von Tonika, Dominante und Subdominante in ihr zusammenklingen. Prinzipiell erscheint die Tonalität in einer Klangfolge, in der die Töne von Tonika, Dominante und Subdominante – in welcher Form auch immer – auftreten. Diese sieben Töne bilden ein harmonisches Ensemble: den Tonbestand einer Tonart.
Der Terminus Tonalität war geschaffen worden, um das harmonische Prinzip der auf Dur- und Molltonarten beruhenden Musik zu benennen. (Fétis hat den Begriff eingeführt als das den Beziehungen der Tonleitertöne zugrunde liegende Prinzip.) Bei der Analyse und Ableitung dieses Prinzips der "Tonartlichkeit" hielt man sich jedoch von vornherein nicht lange auf, sondern löste die Kategorie Tonalität sogleich in die Abstraktion einer "sinnvollen Ordnung" auf, unter der man sich dann alles Mögliche vorstellen konnte. So dachte zum Beispiel Arnold Schönberg, dass die häufigere Wiederholung eines Tons Tonalität begründe, die Vermeidung von Tonwiederholungen also umgekehrt Atonalität. Die harmonische Eigentümlichkeit der tonalen Beziehung ist inzwischen so sehr aus dem Blickfeld geraten, dass das bloße Vorhandensein einer (unbestimmten) Beziehung schon als sachliche Bestimmung anerkannt wird. Es wird demgemäß mit Vorliebe von "Bezogenheit" geredet, und der Unterschied zwischen modaler und tonaler Musik, auf den es bei der Bildung des Begriffs ankam, verschwindet ganz ausdrücklich in den populären Definitionen der Tonalität. Jene wollen nichts mehr davon wissen, dass harmonische Musik und harmonische Tonbeziehungen etwas anderes sind als die Wechselbeziehung zwischen Anhub, Abfall und Rezitationston beim mittelalterlich-kirchlichen Sprechgesang.
Eine zusammenhängende Analyse der Tonalität findet sich in Musikalisches Grundwissen.
Mehr zu diesem Thema auch in dem Artikel Tonalität laut Wikipedia.
|
|
|
|
|
Tonika, Dominante, Subdominante
Tonika, Dominante und Subdominante heißen drei Dur- oder Mollklänge, die im Quintverhältnis stehen und als solche ein harmonisches System bilden, worin die Tonika in der Mitte zwischen Ober- und Unterdominante steht. Der tonale Charakter dieser Klänge existiert nur in ihrer Kombination. Dominante und Subdominante haben untereinander ein über zwei Quinten hinweg gespanntes Verhältnis (9:4), das über die Tonika vermittelt und aufgelöst wird.
Der Begriff Tonika wird gewöhnlich so missverstanden, als ob diese Bestimmung einem Dreiklang (oder gar Ton) als solchem zukomme. Tonika, Dominante und Subdominante sind jedoch Reflexionsbestimmungen, Bestimmungen, die diese Dreiklänge nur durch ihr wechselseitiges Verhältnis haben, also durch jenes harmonische Verhältnis, welches die Tonalität ausmacht.
Die einfache Abfolge von Tonika, Dominante und Subdominante ist eine Kadenz, ihr (partielles) Zusammenklingen eine Dissonanz.
Mehr zu diesem Thema in dem Artikel Tonika laut Wikipedia.
|
|
|
|
|
Abfolge von Subdominante, Dominante und Tonika (abgekürzt: S D T) in der Form von Konsonanzen. Je nach Reihenfolge ergibt sich die authentische Form (T S D T)
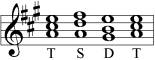
oder die plagale Kadenz (T D S T):

Zu Beginn dieser Beispiele wird die Tonika noch nicht als solche wahrgenommen, weil sie sich noch nicht im Verhältnis zu Dominante und Subdominante präsentiert hat. Erst beim Abschluss der Kadenz erscheint der harmonische Charakter der Tonika. Sie wird dann als Auflösung empfunden, weil sie die harmonische Spannung zwischen Dominante und Subdominante aufhebt, und zwar als ein Klang, der dieser Spannung als vermittelnder Klang zugrunde liegt.
|
|
|
|
|
Die gleichen Klänge, die in der Kadenz aufeinanderfolgen, klingen in der Dissonanz zusammen:
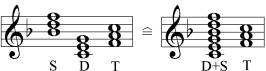
In den obigen beiden Klangfolgen werden jeweils Subdominante und Dominante einander gegenübergestellt und in die Tonika aufgelöst. Die harmonische Sache ist die gleiche. Nur die Form ist verschieden. Auf der rechten Seite erscheint die Konfrontation der Dominanten in einem Zusammenklang und daher als Dissonanz. Die Auflösung der Entgegensetzung von Dominante und Subdominante nimmt daher die Form der Auflösung einer Dissonanz an.
Die Dissonanz unterscheidet sich also dadurch von der Konsonanz, dass sie ein tonales Verhältnis in sich enthält. Sie ist kein Zusammenklang von unmittelbar harmonierenden Tönen, sondern von Tönen, die als Bestandteile der tonalen Dreiklänge harmonieren. Dabei müssen nicht immer alle Bestandteile eines Dreiklangs in einer Dissonanz vorkommen. Die Dissonanz kann beliebige Einzelteile von Tonika, Dominante und Subdominante in sich vereinigen, so dass es eine ganze Reihe von Dissonanzen gibt, die man je nach Zusammensetzung in verschiedene Gruppen einteilen kann. Beispiele mit harmonischer Formel in F-Dur:
1. Zusammenklänge von Dominante und Subdominante:

2. Zusammenklang von Tonika, Dominante und Subdominante in einer Klangfolge mit Auflösung in die Tonika:
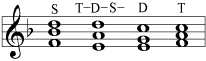
3. Zusammenklänge von Tonika und Dominante oder Subdominante:
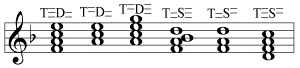
Je nach tonaler Charakteristik ist das, was man als Auflösung einer Dissonanz bezeichnet, teils die Auflösung des Gegensatzes der Dominanten (wie in der Kadenz), teils aber auch die Herauslösung der Tonika aus ihrem Verbund mit der Ober- oder Unterdominante.
Ihrer Harmonik nach unterscheiden sich die Dissonanzen wesentlich nach ihrer Zusammensetzung. Ihrer Form nach unterscheiden sie sich in markante Dissonanzen, die schon für sich genommen ihren dissonanten Charakter preisgeben, und Scheinkonsonanzen. Aber auch markante Dissonanzen lassen für sich genommen nicht immer ihre harmonische Zusammensetzung eindeutig erkennen. Dies wird besonders deutlich bei Betrachtung der Schwingungsverhältnisse, in denen das Zusammenklingen der Töne in der Dissonanz resultiert:
Es zeigt sich an den obigen Beispielen,
-
dass unterschiedliche Dissonanzen die gleichen Schwingungsverhälnisse haben können,
-
dass harmonisch identische Dissonanzen unterschiedliche Schwingungsverhältnisse haben können,
-
dass unterschiedliche Dissonanzen wegen ihrer akustischen Ähnlichkeit oder Übereinstimmung die gleiche Bezeichnung haben können.
Die Schwingungsverhältnisse, in denen sich harmonische Verhältnisse darstellen, sind keineswegs das, was die Eigenart der Harmonien begründet. Schon die bloße Form des quantitativen Verhältnisses bringt jeglichen qualitativen Unterschied zum Verschwinden. Das Verhältnis 16:5 enthält größere Zahlen als das Verhältnis 9:5 oder 6:5. Dies besagt jedoch nichts über Konsonanz und Dissonanz. Selbst der Versuch, von den puren Schwingungsverhältnissen auf die sich darin ausdrückende Harmonie zu schließen, kann wegen der vielfältigen Verwechslungsmöglichkeiten nur ausnahmsweise gelingen. Harmonien bewähren sich als das, was sie ihrem Begriff nach sind, nur in der Abfolge von Klängen, in denen sich die Entgegensetzung der Dominanten und die Auflösung in die Tonika vollzieht. Harmonien sind wesentlich Momente dieser tonalen Bewegung.
Die gängige Verwechslung von Harmonie und Schwingungsverhältnis findet ihren Niederschlag in der Rede von den Sonanzgraden.
Mehr zu diesem Thema in dem Artikel Dissonanz laut Wikipedia
.
|
|
|
|
|
Häufig vorkommende Dissonanz, in der die Dominante mit dem Grundton der Subdominante zusammenklingt.

Wie alle Dissonanzen, so wird auch der Dominantseptakkord in die Tonika aufgelöst. Der Name Septakkord enthält die Ordnungszahl sieben. Das kommt daher, dass die Töne der Kadenz, sobald man sie der Tonhöhe nach anordnet, zu Tönen einer Tonleiter werden. Darin erscheint dann der subdominantische Grundton, vom dominantischen Grundton aus gerechnet, als siebte Stufe. Der Name enthält also eine Vermischung der harmonischen ("Dominant-") mit der melodischen Betrachtungsweise ("-sept").
Da diese Erkenntnis nicht sehr verbreitet ist, haben Zitate wie das folgende Seltenheitswert:
"Gerade in dem Dominant-Septimenakkord ... erblicken wir denjenigen Zusammenklang, den wir direkt als den Typ einer Dreiklangs-Mischharmonie ansehen können; ... seiner wahren Natur nach besteht der Dominant-Septimenakkord nämlich aus dem tonartlichen Oberdominant-Dreiklang, dem der um zwei Oktaven nach oben verlegte Grundton des Unterdominant-Dreiklangs sich hinzugesellt ..." (Max Paul Heller, Die Musik als Geschenk der Natur, Berlin 1930, S. 60).
|
|
|
|
|
Dissonanz in Moll, in der Terz und Quinte der Dominante mit Grundton und Terz der Subdominante zusammenklingen. Harmonische Formel und ein Beispiel in a-Moll:
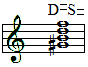
Diese Dissonanz wird auch Septakkord der 7. Stufe in Moll genannt. Prinzipiell sind die Namen der Harmonien nicht aus einem Wissen um ihre harmonische Zusammensetzung abgeleitet, sondern aus der melodischen Vorstellung von Intervallen. In diesem Fall kursiert noch immer die traditionelle Auffassung, der Akkord sei aus drei kleinen Terzen aufgebaut, die zusammen eine (um einen Halbton) verminderte Septime ergeben.
|
|
|
|
|
Der Tritonus ist eine markante Dissonanz (im Unterschied zur Scheinkonsonanz), und zwar schon als der bloße Zweiklang, der er ist. Hier ein Beispiel:

Die Bezeichnung Tritonus kommt daher, dass man sich diesen Zweiklang ursprünglich als Resultat aus drei Ganztonschritten vorgestellt hat. Er wird auch verminderte Quinte genannt (so in der obigen Tabelle der Dissonanzen), womit genaugenommen aber nur das Intervall zwischen den Tönen dieses Zusammenklangs gemeint ist. Seiner harmonischen Natur nach handelt es sich um die Kombination von dominantischer Terz und subdominantischem Grundton (kurz gefasst durch die harmonische Formel über dem obigen Notenbeispiel). Das Frequenzverhältnis errechnet sich so: Vom Grundton der Subdominante zu dem der Dominante sind es zwei Quinten, also 3:2 × 3:2. Die Terz hat dann das Verhältnis 5:4. Setzt man den oberen Ton eine Oktave tiefer, so ergibt sich:
3:2 × 3:2 × 5:4 × 1:2 = 45:32
Da der Tritonus nicht mit einer Konsonanz verwechselbar ist, weil er auch als isolierter Klang auflösungsbedürftig erscheint, wird er oft als Ursache jeglicher Dissonanz angesehen, in der er vorkommt. So soll er angeblich auch die Auflösungsbedürftigkeit des Dominantseptakkords begründen. Seinen dissonanten Charakter versucht man aus dem Zahlenverhältnis 45:32 zu ergründen. Man ist also auf der Suche nach einem im Zahlenverhältnis liegenden Geheimnis der Dissonanz. Der qualitative Unterschied zwischen Konsonanz und Dissonanz, an dem man die Frage der Auflösungsbedürftigkeit eines Klangs entscheiden will, soll in quantitativen Verhältnissen zu suchen sein. Dieser Unterschied soll durch eine „Grenze“ gefunden werden, die kleine und große Zahlen trennt. Auf diese Weise will man auf geheimnisvolle Weise „einfache“ Proportionen von „komplexen“ scheiden. Die musikalische Erklärung der Dissonanz wird in eins gesetzt mit einer Suche nach mathematischen und physikalischen Ursachen. Man verwickelt sich in Widersprüche und konstruiert immer wieder neue Theorien, kann aber die ominöse „Grenze“ bei den Schwingungszahlproportionen nicht finden. Die Fixierung auf Zähl- und Messbares liefert immerzu nur fortlaufende Reihen und keine harmonischen Bestimmungen. Aber die solchermaßen unsachgemäße Untersuchung der Dissonanz wird auch nirgends als Irrweg erkannt. Aus der nicht gefundenen „Grenze“ wird dann auf die Nichtexistenz des zu erklärenden Unterschieds geschlossen. Demnach gibt es nur fließende Übergänge, wo doch Klänge danach unterschieden werden sollten, ob sie auflösungsbedürftig sind oder nicht. Die wissenschaftliche Ratlosigkeit und die Befangenheit in sich widersprechenden Aussagen schlagen sich auch in Lexikon-Artikeln wie dem folgenden nieder:
„Konsonanz“ ist „in tonaler Musik ein Klang
(Intervall oder Akkord) mit Ruhe- und Entspannungscharakter im Gegensatz zur auflösungsbedürftigen Dissonanz.
Die Töne konsonanter Klänge stehen zueinander in einfachen Schwingungszahlproportionen.
Allerdings läßt sich das Konsonanzphänomen weder mathematisch noch physikalisch eindeutig erklären.
Denn die Konsonanz ist keine feststehende Größe, sondern ein relativer Klangwertbegriff,
zudem ihrem Grad nach abgestuft und ohne klar bestimmbare Grenze zur Dissonanz (...).“
(Gerhard Kwiatkowski u. a. (hg.), Meyers kleines Lexikon Musik, Mannheim u. a. 1986, S. 186)
Wenn man nicht nach außermusikalischen (mathematischen, physikalischen,
psychologischen ...) Erklärungen für musikalische Klänge sucht, kommt man
dem Unterschied zwischen Konsonanz und Dissonanz keichter auf die Spur:
Der Unterschied besteht einfach darin,
dass im einen Fall Tonika, Dominante und Subdominante nur mit ihren eigenen
Tönen erklingen und im andern Fall die Töne dieser Klänge sich vermischen.
![]()
![]()
![]()
![]()
Dissonanz, die für sich genommen, also außerhalb des harmonischen Zusammenhangs, in dem sie steht, wie eine Konsonanz klingt. Ihr dissonanter Charakter und ihre Auflösungsbedürftigkeit zeigt sich nur in Klangfolgen, in denen sich die Harmonik der Tonalität entfaltet. Beispiel: die 2. Harmonie in dieser Klangfolge:

|
|
|
|
|
Für die harmonische Analyse der Dissonanzen ist es zweckmäßig, Grundton, Terz und Quinte als Striche hinter den Kürzeln von Tonika, Dominante und Subdominante zu notieren. Die Striche symbolisieren die Lage der Töne in der Grundform des Dreiklangs: Der Grundton wird in dieser harmonischen Formel unten notiert, die Quinte oben. Beispiel: ein Zusammenklang der Grundtöne von Dominante und Subdominante:
![]()
|
|
|
|
|
Die gewöhnliche Vorstellung von Konsonanz und Dissonanz beruht auf dem Widerspruch, einen qualitativen Unterschied zwischen beiden zu unterstellen und ihn zugleich durch die Behauptung eines bloß quantitativen Unterschieds zu tilgen. Dabei wird selbst der Ausgangspunkt der Unterscheidung von Konsonanz und Dissonanz – die Sache mit der Auflösungsbedürftigkeit der Dissonanz – verkehrt gefasst: Der Unterschied wird nicht in der Form des Harmonierens festgehalten, sondern in eine Frage von "Missklang" und "Wohlklang" umgedeutet. In Zahlenverhältnissen (worin Konsonanz und Scheinkonsonanz [eine Dissonanz!] sogar übereinstimmen können), wird dann der Grund des Unterschieds gesucht, und zwar in Form einer Grenze zwischen kleinen und großen Zahlen, wobei die Grenze dann wieder vom Zeitgeschmack abhängen soll. Oder es wird eine geheimnisvolle qualitative Besonderheit an den quantitativen Verhältnissen gesucht. Da Zahlen aber letztlich doch nur quantitative Unterschiede aufweisen, mündet die Identifizierung von Harmonie und Zahl einerseits in Zahlenmystik –
"In ihrem Kern ist Musik reine Mathematik – berechenbare Luftschwingungen, deren Frequenzen sich nach physikalischen Regeln überlagern. Und doch geschieht eine Art Wunder: Mathematik verwandelt sich in Gefühl." (DER SPIEGEL 31/2003)
– andererseits in die Leugnung des qualitativen Unterschieds von Konsonanz und Dissonanz:
"Der Unterschied zwischen ihnen ist daher nur graduell und nicht wesentlich. Sie sind, was sich ja auch in den Schwingungszahlen ausdrückt, ebensowenig Gegensätze, wie zwei und zehn Gegensätze sind; und die Ausdrücke Konsonanz und Dissonanz, die einen Gegensatz bezeichnen, sind falsch." (Arnold Schönberg, Harmonielehre, Wien 2001)
Ein verbreitetes Verfahren, den qualitativen Gegensatz von Konsonanz und Dissonanz in quantitative Unterschiede aufzulösen, besteht in der Unterstellung, den Zahlen könnten steigerungsfähige Qualitäten wie "einfach" und "kompliziert" zugeschrieben werden. Dann lässt sich mit etwas Geschwafel und durch Weglassen der Vorsilben Kon- und Dis- das Konstrukt der "Sonanzgrade" postulieren, ein geheimnisvolles Etwas, von dem die Harmonien gewisse Portionen enthalten sollen und denen man sogar eine geheimnisvolle Ursache unterstellen kann:
"Die Einfachheit oder Kompliziertheit der Zahlenproportionen ist ein Symbol (keine Erklärung), die größere oder geringere Verschmelzung der Töne im Zusammenklang ist ein sinnliches Merkmal, die Koinzidenz von Obertönen ist (vielleicht) die oder eine Ursache der Sonanzgrade." (Carl Dahlhaus, Konsonanz-Dissonanz, Die Musik in Geschichte und Gegenwart, Kassel 1996).
|
|
|
|
|
Das Harmonieren von Tonika, Ober- und Unterdominante, das die Tonalität ausmacht, erscheint in Musikstücken zuweilen (oft an Anfang oder Ende) in der einfachen Form der Kadenz, meist jedoch in einer Folge von Konsonanzen und Dissonanzen. Die beständige Entgegensetzung der Dominanten und ihre Auflösung in die Tonika – oder kurz: die tonale Bewegung – vollzieht sich also, wenn man von ihren verschiedenen Verlaufsformen absieht, im Auftreten der Töne von Tonika, Dominante und Subdominante. Diese insgesamt sieben Töne bilden den Tonbestand einer Tonart. Als solche bringen sie die harmonischen Verhältnisse der Tonalität ins Spiel, an denen sich entscheidet, welche Tonart gerade gespielt wird. Dies ist auch der Grund, warum es nur Dur- und Molltonarten nach folgendem Schema gibt:


Eine Durtonart besteht aus drei Durklängen, eine Molltonart aus zwei Mollklängen und einem Durklang. Dur- und Mollklänge können keinesfalls beliebig zu Tonarten kombiniert werden. Beim Versuch, drei Mollklänge zu einer Moll-Tonalität zusammenzufügen, ergibt sich aufgrund des verwendeten Tonbestands eine Scheintonalität, die aus Scheinkonsonanzen besteht (kenntlich an den Formeln) und die mit einer Tonika in Dur aufgelöst wird:
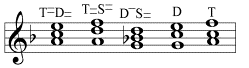
Die Durchsetzung der Tonart F-Dur im obigen Tonbestand beruht auf der stärkeren Konsonanz des Durklangs, dessen Teiltöne eine größere Übereinstimmung aufweisen als die des Mollklangs. In den Anfängen der Tonalität blieb dies noch unerkannt: Jahrhundertelang wurde mit den Kirchentönen – also mit dem Tonbestand einer modalen Musik – mehrstimmige Musik gemacht, die sich vom harmonischen Standpunkt aus als Scheintonalität erweist. Erst die Renaissance-Musik setzte allmählich das gis (statt g) in a-Moll durch und entwickelte die modernen Tonarten, die in jedem Fall einen Durklang zur Dominante haben.
Übrigens geht auch der Versuch, eine Moll-Tonalität mit einem Durklang als Subdominante zu konstruieren, immer schief: Es zeigt sich dann eine Scheintonalität, die ebenfalls durch eine Tonika in Dur aufgelöst wird:
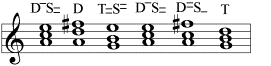
Die Verwandtschaft der Tonarten ist ein harmonischer Sachverhalt, um den es bei der Modulation geht.
|
|
|
|
|
| © 2016 Franz Sauter, Hamburg | Datenschutz |